两个业余数学家推翻300年猜想300年数学定律被推翻
一个300多年的难题，居然被两个业余数学家推翻了！
网友感叹：数学家真不容易，花那么多时间来证明一个不能马上产生经济效益的东西。【图1】
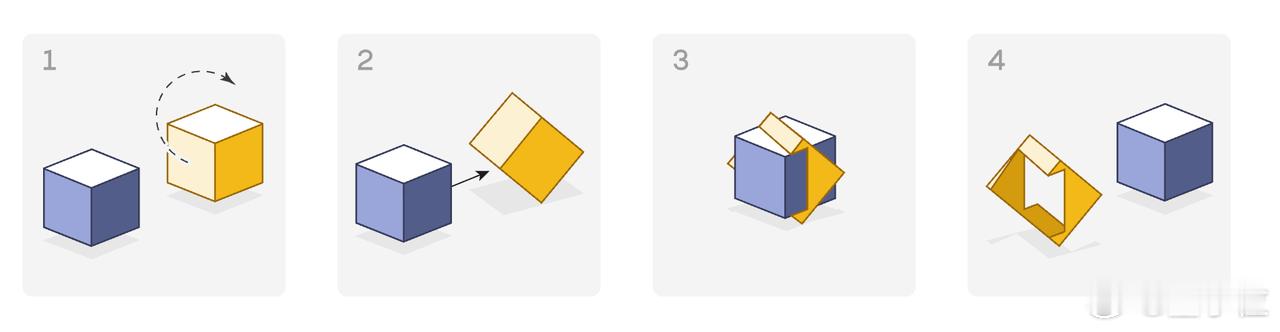
故事是这样的：300多年前，有人跟鲁珀特亲王打赌，说两个骰子不可能一个穿过另一个。结果亲王赢了。
后来数学家用理论和实物都证明了：只要顺着立方体的内对角线打个洞，另一个同尺寸的立方体就能完整穿过，留的空隙甚至还能再大4%。
这种能力后来被称为“鲁珀特特性”（Rupert Property），也就是：某个形状能不能钻个直洞，让另一个完全相同的自己穿过去。
几百年来，研究者陆续发现越来越多的多面体都拥有这个能力，包括立方体、正四面体、正八面体、足球（截角二十面体）等等。于是一个大胆的猜想出现了——是不是所有的“凸多面体”都有这项特性？
但现在，这个猜想被击碎了。
两位数学爱好者Steininger和Yurkevich发现了一个真正“穿不过自己”的形状，他们把它命名为——Noperthedron（Nope+Rupert）。这是第一个被严格数学证明无法拥有鲁珀特特性的形状。
Noperthedron长这样：有90个顶点、152个面（其中150个是三角形，两个是正15边形），看起来像个胖胖的水晶花瓶。目前已经有人3D打印出来当笔筒用了。
要证明一个形状不能穿过自己，并不是找不到“洞”就行，而是要能排除所有可能的角度和方向。
他们的做法是：
- 把所有可能的朝向想象成一个高维的“参数空间”；
- 用“全局定理”大范围排除一整片区域；
- 用“局部定理”排除那些几乎重合、只差一点点的小角度；
- 把整个参数空间划成1800万个小区块，用计算机一个个验证；
最终结果是：所有方向都不行。
这个结果，不只是为Noperthedron定了性，更是第一次证明——确实存在一些形状，是永远无法穿过自己的。
几百年的直觉猜想被推翻，而这背后，是两个非学术背景数学爱好者5年的坚持。他们说，他们研究这件事的方式，就是“吃着披萨+聊着数学”。
也许人类能解决最硬核问题的方式，远比想象中朴素。
